作図問題１　 2000.5.23

　この作図のルールは、

（１）コンパスと定規だけを使う
（２）コンパスは円を描くことのみに使い、定規は直線を引くことのみに使う

　古代ギリシャの時代からあった古ーい学問です。ちなみにギリシャの３大作図問題というものがあります。

    ａ）与えられた角を三等分すること（角の３等分問題）
    ｂ）立方体の二倍の体積をもつ立方体の一辺を作図すること（立方体倍積問題）
    ｃ）円と等積な正方形を作図すること（円の正方形化問題・円積問題）

　学者や、数学マニアのおともだちが、みーんな挑戦しては敗れていったという問題ですが、１９世紀になってから作図不能であることが証明されたんだそうです。
（ikuro's Homepageの数学コラム「不可能の証明」 ）

図形の問題って、数学っていうよりパズルに近いので、ヒマなときにやってみると楽しいかもしれません。（いろいろな問題を解いてみたいというお友達は、「数学の部屋」にどうぞ。）

（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）（＾＾）

　さてさて、今回は「コンパスと定規だけを使って、キティさんを描いてみよう」という問題に挑戦してみることにしました。
 

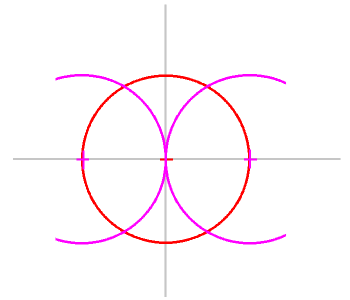	１．縦線と横線を引きます。 　　（垂線の引き方はわかるよね？） ２．交点を中心とした円を描きます。（左図の赤い円） 　　（この大きさが、ほぼキティさんの顔の大きさになります） ３．横線と赤い円との交点を中心とした円を描きます。（ピンクの円） 　　半径は赤い円と同じです。
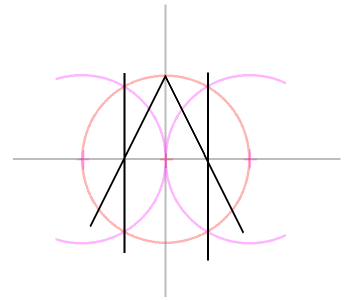	４、補助線を４本引きます。 　４−１　赤い円とピンクの円の交点を結びます。 　４−２　赤い円と縦線との交点から、（４−１）で引いた線と横線との交点を通る 　　　　　 線を引きます。（ややこしいなあ（＾＾；）
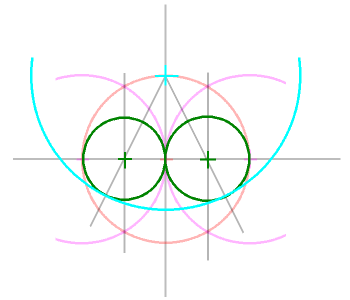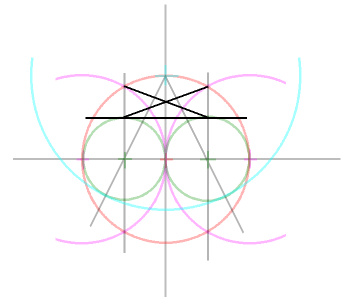
	５、いま引いた補助線の交点を中心とし、赤い円に内接する円を描きます。（緑の円） 　　（つまり、赤い円の半径の半分の円ですね） ６、４で引いた斜めの線の交点を中心とし、（５）で描いた円（緑の円）に内接する円を描 　　きます（水色の円）。
	７、ここでまたまた補助線を引きます。 　　（４）で引いた補助線（縦線）と、赤い円、緑の円との交点を、左図のように結びます。 　　横線は、赤い円に交わるところまで伸ばしておきましょう。
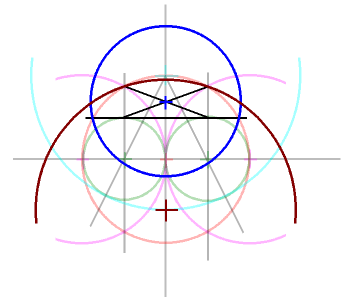	８、（７）で引いた補助線の×の交点を中心とし、横線と赤い円との交点を通る円（青い円）を描きます。 ９、つづいて、最初に描いた補助線と、（６）で描いた水色の円との交点を中心とし、赤い円とピンク円 　　との交点を通る円（茶色の円）を描きます。
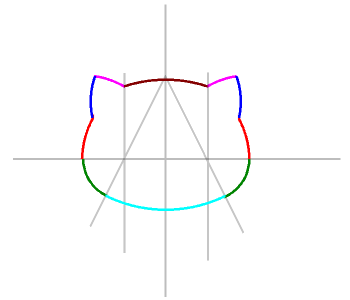	１０、余分な線を消すと、あら不思議、キティさんになってしまいました。ふっしぎー♪

．．．これでやっとキティさんの顔の輪郭が描けました。
なお、最後の出来上がりの状態を頭においておき、円弧の必要な部分だけを描くようにすれば、あとで消す手間が大幅に減るというものです。

　あとは、目鼻をつけて、おヒゲ描いて、耳リボンをつければ完成ですが、それは次回のおたのしみ．．．